Як уже відомо, в прямокутному трикутнику синус гострого кута визначається як відношення протилежного катета до гіпотенузи, а косинус гострого кута — як відношення прилеглого катета до гіпотенузи. Оскільки радіус півкола R = AO = 1, то sin α = AX ; cos α = OX .
У визначеному трикутнику, синус кута дорівнює довжині протилежного катету поділеному на довжину гіпотенузи (інші тригонометричні функції можуть визначатися аналогічним способом; наприклад, косинус кута є відношенням довжин прилеглого катету до гіпотенузи).
Якщо α – тупий кут (рис. 4), то cos α = ОС = – OD = -cos (180°- α), sinα = AC = AD = sin (180° – α), тоді tg α = = – = -tg(180° – α). Отже, щоб знайти синус тупого кута, досить знайти синус суміжного кута; щоб знайти косинус, тангенс тупого кута, треба знайти число, протилежне косинусу, тангенсу суміжного кута.
Щоб знайти катет, протилежний до гострого кута прямокутного трикутника, потрібно гіпотенузу помножити на синус цього кута, або прилеглий катет помножити на тангенс цього кута.
Сума синусів двох кутів дорівнює подвоєному добутку синуса півсуми цих кутів на косинус їх піврізниці.
Синусом гострого кута прямокутного трикутника називають відношення протилежного катета до гіпотенузи. Синусом гострого кута прямокутного трикутника називають відношення прилеглого катета до гіпотенузи.

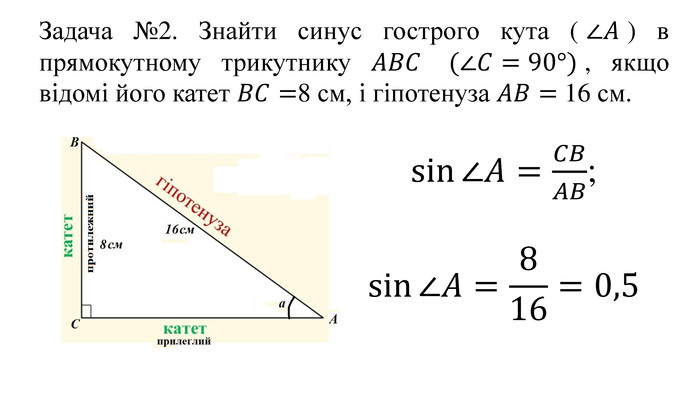
Наступні приклади вирішуються з використанням вивченого про синус кута. Кожен приклад має відповідне розв’язання, але рекомендується спробувати вирішити задачі самостійно, перед тим як переглядати рішення. Отже, за формулою синуса для прямокутного трикутника маємо: …
